Have you ever heard someone say, “When you multiply, your product is always greater than your factors”, “When you divide, your quotient is always less than your dividend and divisor.” Are these statements always true? Are we inadvertently teaching misconceptions to our students by stating these “rules?”
If you multiplied 3 x 1/3, would the product be greater than the factors?
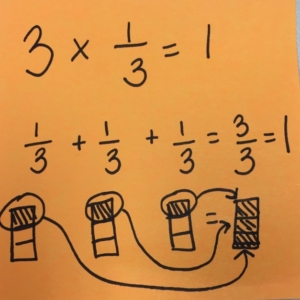
Many students are taught that when you multiply your product is always greater than your factors, but that rule only applies when you are working with positive whole numbers. When fractions, decimals and negative numbers are later introduced, the rule is no longer true.
How about when you divide 2 and 1/2? Would the quotient be less than the dividend and divisor?
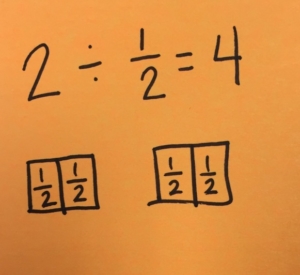
When students first learn about division they focus on the partitive understanding, that when you are sharing a quantity you cannot have more than what you started with. However, that rule expires when you begin dividing whole numbers and fractions/decimals and fractions by fractions or decimals by decimals.
Karp, Bush, and Dougherty, state, “Overgeneralizing commonly accepted strategies, using imprecise vocabulary, and relying on tips and tricks that do not promote conceptual mathematical understanding can lead to misunderstanding later in students’ math careers.” Check out this article written by Karp, Bush and Dougherty, on more rules that expire in Math! http://www.scusd.edu/sites/main/files/file-attachments/13_rules_that_expire_0.pdf