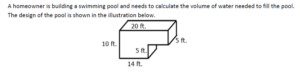
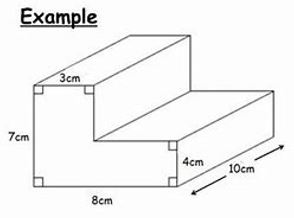
Relate volume to the operations of multiplication and addition and solve real world and mathematical problems involving volume.
a. Find the volume of a right rectangular prism with whole-number side lengths by packing it with unit cubes, and show that the volume is the same as would be found by multiplying the edge lengths, equivalently by multiplying the height by the area of the base. Represent threefold whole-number products as volumes, e.g., to represent the associative property of multiplication.
b. Apply the formulas V = l × w × h and V = B × h for rectangular prisms to find volumes of right rectangular prisms with whole-number edge lengths in the context of solving real world and mathematical problems.
c. Recognize volume as additive. Find volumes of solid figures composed of two non-overlapping right rectangular prisms by adding the volumes of the non-overlapping parts, applying this technique to solve real world problems.
[divider] [/divider]
Students are able to…
- Understand that the volume of an object can be measured by finding the total number of same-sized units required to fill the space without any gaps or overlaps.
- Measure volume of a rectangular prism by filling only the base with cubes and determining the other two dimensions of the prism using the cubes given.
- Discuss more efficient ways to find the volume than to use cubes to fill in the prism.
- Understand and apply the formulas V = l x w x h and V = b x h for rectangular prisms in real world problems to find volumes with whole number edge lengths.
- Apply a formula for volume to find the volume of composite figures where two rectangular prisms are attached and students must find the volume of the entire figure.
Students are able to…because teachers:
- Plan activities where students find the volume of several rectangular prisms by counting cubes.
- Plan questions to prompt students to consider how to find the volume if they have only enough cubes to cover the bottom of the rectangular prism but not enough cubes to fill the entire prism.
- Facilitate discussion about finding more efficient ways to calculate volume.
- Model appropriate use of measurement vocabulary terms such as attribute, volume, solid figure, rectangular prism, unit, unit cube, gap, overlap, cubic units, addition, multiplication, edge lengths, height, and area of base. Encourage students to use measurement vocabulary.
[divider] [/divider]
Questions to ask students:
- How can you find the volume of a box if you do not have any cubes? Is there more than one way?
- Sample answer that indicates understanding: Measure the length, width, and height and multiply the length by the width by the height. You can also find the area of the base and multiply that by the height.
- Sample answer that indicates an incomplete understanding or a misconception: Find the length of two edges of the bottom of the box.
- What strategy can you use to find the volume of a composite figure (two figures put together to make one figure)?
- Sample answer that indicates understanding: Find the volume of each of the prisms separately then add them together.
- Sample answer that indicates an incomplete understanding or a misconception: Find the length, width, and height of the whole figure and multiply them using the volume formula.
[divider] [/divider]
FSA Notes
Cognitive Complexity Level: Level 2: Basic Application of Skills & Concepts
Achievement Level Descriptors:
Level 2: solves volume problems of a right rectangular prism by using unit cubes
Level 3: relates the number of unit cubes in a rectangular prism to the multiplication of the height to the area of the base or the multiplication of the edge lengths; solves real-world and mathematical problems by applying the formulas for volume
Level 4: finds the volume of two non-overlapping right rectangular prisms by adding the volumes of the two non-overlapping parts
Level 5: finds a missing dimension of a rectangular prism given two dimensions and the volume; generates possible dimensions of a rectangular prism given the volume
Assessment Limits:
Items may not contain fraction or decimal dimensions or volumes.
Items may contain no more than two non‐overlapping prisms – non‐overlapping means that two prisms may share a face, but they do not share the same volume.
Items assessing MAFS.5.MD.3.5b may not contain the use or graphic of unit cubes.
Items assessing MAFS.5.MD.3.5c must contain a graphic of the figures.
[divider] [/divider]
Additional Resources:
Additional In depth content knowledge
Videos:
LearnZillion: Find Volume by Multiplying the Area of the Base by the Height
Learnzillion: Volume of Complex Rectangular Prisms
Khan Academy: Volume through Decomposition
[divider] [/divider]
Sample Formative Assessment Tasks:
[divider] [/divider]
[divider] [/divider]
[divider] [/divider] Resources/Tasks to Support Your Child at Home:
- Look around the house for objects that are shaped like rectangular prisms. For example: cereal boxes, tissue boxes, shoeboxes, etc. Measure the length, width and height of each rectangular prism to the nearest inch, foot, or centimeter. Use the measurements to calculate the volume of each.
Guiding Questions:
How did you find the volume of each prism?
What does B mean in the volume formula?
[divider] [/divider]
Find the volume of rectangular prisms found at home: cereal box, tissue box, shoe box, etc. Find and compare the volume of rectangular prisms (boxes) found. Put two prisms together. Find the volume of the new shape.
[divider] [/divider]
What is one way to decompose this complex figure into two rectangular prisms?
What is another way this figure could be decomposed?
What is the volume of the complex figure?