Fluently multiply multi-digit whole numbers using the standard algorithm.
[divider] [/divider] Students are able to…
- Estimate the product before solving to help determine if their solution is reasonable.
- Connect strategies like partial products and area model to the standard algorithm.
- Explain their reasoning when using the standard algorithm, which should include use of the properties of multiplication and place value.
[divider] [/divider] Students are able to…because teachers:
- Provide a variety of activities and experiences in which students multiply multi-digit whole numbers explicitly connecting strategies like partial products and area model to the standard algorithm.
- Present students with various problem solving situations for multiplication.
- Facilitate student discussions in which they explain how thinking about numbers flexibly and using conceptual strategies help us understand the standard algorithm for multiplication.
[divider] [/divider] Questions to ask students:
- Ask a student who estimated and then solved if their solution is reasonable and how they know if it is reasonable or not.
- Ask students why they wrote a zero before multiplying the second partial product (Example: 372 x 46)
- Sample answer that indicates understanding: Before multiplying the second partial product I write a zero because I’m not multiplying 372 x 4, I’m multiply 372 x 40. The zero is needed to reflect the actual value of the 4.
- Sample answer that indicates an incomplete understanding or misconception: Before you multiply the second partial product you must write a zero to get the correct answer.
- Ask students why the second partial product in the standard algorithm is always greater than the first when multiplying by a 2-digit number.
- Sample answer that indicates understanding: The second partial product is always greater because now we are multiplying a number with a value in the tens place, when before we were multiplying a number with only a value in the ones place.
[divider] [/divider] FSA Notes
Cognitive Complexity Level: Level 1- Recall
Achievement Level Descriptors:
2: multiplies two two-digit numbers using the standard algorithm
3: fluently multiplies two-digit by up to five-digit numbers using the standard algorithm
4: determines the missing digit in a factor of a multiplication problem when given the product
5: analyzes an error in the multiplication computation using the standard algorithm and justifies the reasoning
Assessment Limits: Multiplication may not exceed five digits by two digits.
[divider] [/divider]
Additional Resources:
Additional in depth content knowledge:
Video Lesson: Connecting Partial Products to the Standard Algorithm
Video: Multiplying multi-digit numbers using the standard algorthm
[divider] [/divider]
Sample Formative Assessment Task:
[divider] [/divider] Resources/Tasks to Help Your Child at Home:
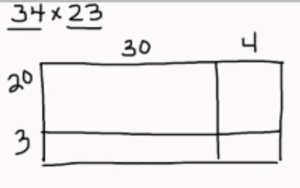
Task: What are some strategies to find the product of 34 x 23?
Task: Look at this strategy that was started how does it connect to the standard algorithm for multiplication?
Kahn Academy Video: Connecting the Area Model to the standard algorithm for multiplication https://goo.gl/84RB2X
Learn Zillion Video: Connecting partial products to the standard algorithm for multiplication https://goo.gl/uPbKY5
Task: Provide multiple opportunities for your child to practice:
376 x 8
26 x 28
263 x 37
9,246 x 14
35,082 x 62
Kahn Academy Video: Using the standard algorithm for multi-digit multiplication https://goo.gl/NnfzoL
Task: The shirt store sells shirts in whole dollar amounts starting at $5.00. If you were going to buy 82 of the same t-shirts for the 5th grade class and you could spend up to $1100, what is the most you could spend on one shirt?
Task: Use estimation to explain how you know there is an error in the equation below:
32 x 84 = 393
Kahn Academy Video: Example of using estimation to find a near product https://goo.gl/YCg538