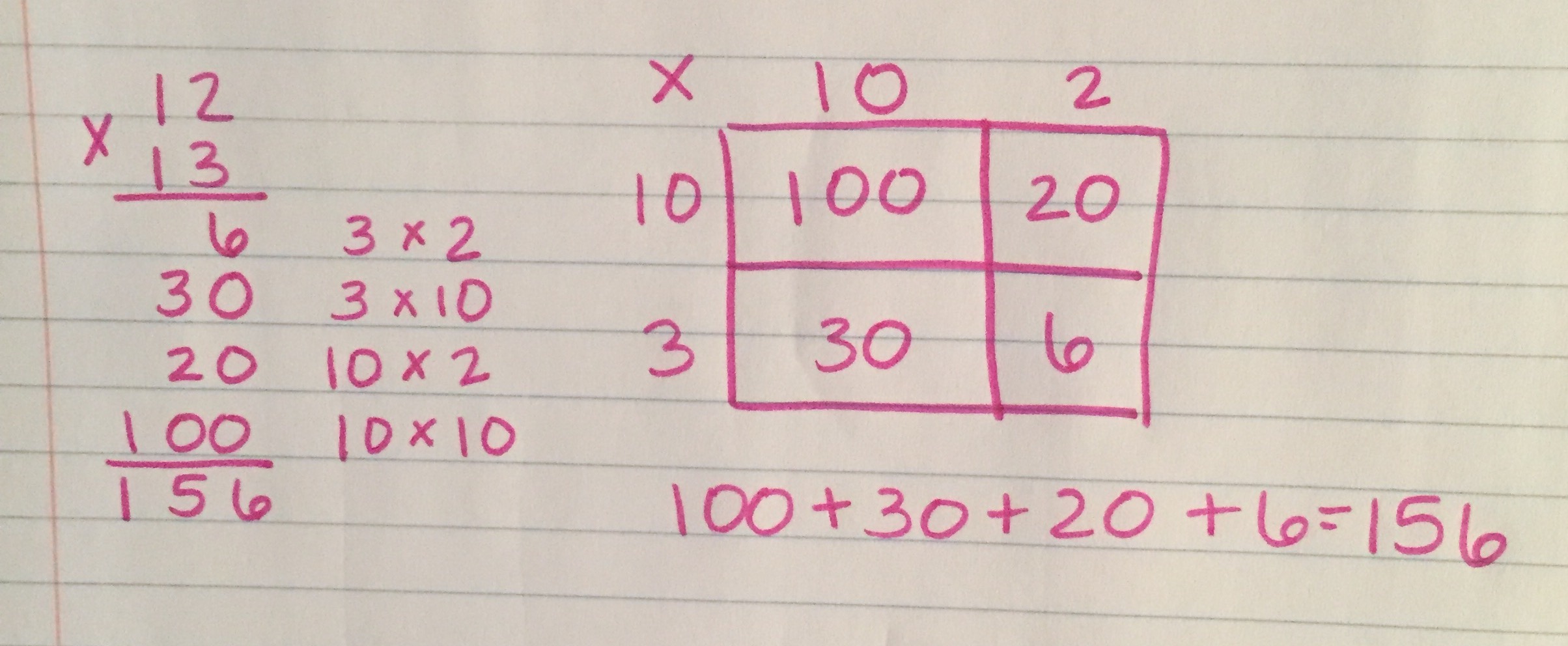MAFS.4.NBT.2.5 states that 4th graders should be able to:
Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
When introducing multi-digit multiplication, the tendency is to dive right in to the standard algorithm. While the standard algorithm is an efficient strategy, it is very procedural and many kids copy performing the steps without understanding the process, which can result in misconceptions that are difficult to undo. A great approach for building conceptual understanding is to begin with base-ten models, and then connect those models to the partial products method and area model. This ensures that students have an understanding of all parts of the standard.
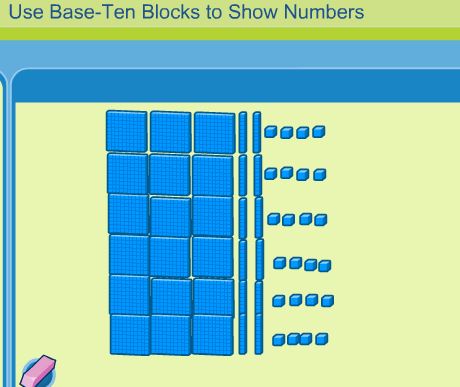
You can see from the following examples of 324 x 6 the similarities in the three methods. The area model is just a pictorial representation of the base-ten model, while partial products is a more abstract way of recording both strategies. All strategies are rooted in the student’s understanding of place value. The standard algorithm is actually a short-cut method of partial products, and fluency with the standard algorithm is a 5th grade standard. (https://www-k6.thinkcentral.com/content/hsp/math/hspmath/na/gr3-5/itools_intermediate_9780547274058_/basetenblocks.html virtual base-ten blocks were used to create the base-ten model.)
Students see that to multiply 324 x 6, they actually multiply 6 times the ones, 6 times the tens, and 6 times the hundreds. These strategies allow students to break larger problems down so they can work with their basic facts and multiples of 10 and 100.
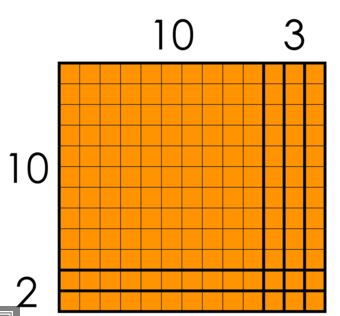
The area model is a great opportunity to make connections to arrays and students’ experience in 3rd grade with area.
All three strategies can also be applied when multiplying two 2-digit numbers, as shown in the representations of 12×13 shown below.
🙂