Functions can be overwhelming with all of the f’s, x’s, and f(x)’s. But in reality, functions are quite easy to understand once you know how they work.
So what is a function? Well, a function can be described as a relation from a set of inputs to a set of possible outputs where each input is related to exactly one output. Think of a function as a fortune telling machine. If you fill out a card with your first name and birthday and then feed the card into the machine you will receive your fortune. It is important to note that in order for this to be a function, the same name and birthday combination will receive the same fortune as you. Think about it this way: If it were truly a fortune machine, why would you expect to get a different fortune if you did it 3 times in a row? You wouldn’t!
In math class, the information that you feed the machine is called the input or x. Your fortune is called the output or the function of x. The functional notation for this is f(x) although other variables can be used such as g(x) or h(x). As outputs are generated, a table can be used to visually display the values.
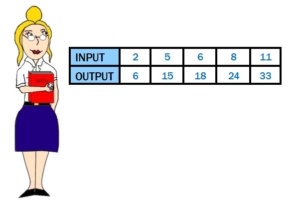A function is the mathematical computation(s) in between the input and output. In this example, we need to determine what happened to the input to get the corresponding output. Each input was multiplied by 3. Therefore, the function is f(x)= 3x. A common error occurs when only the inputs or outputs are compared. While a pattern may be seen, it is important to make the connection between the input and output.
Want to have some fun? Check out this interactive function machine where you guess the function!