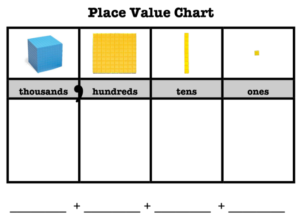
Leaning the base ten system is like learning a new language for our children. Instead of letters there are the digits 0-9. Depending on the placement of the digit determines the value it represents. We group 10 ones to make 1 ten, 10 groups of ten to make 1 hundred and so on. This repeated pattern needs to be explored in many ways for children to build a deep and flexible understanding of the base ten system.
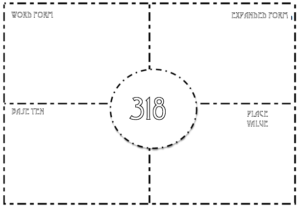
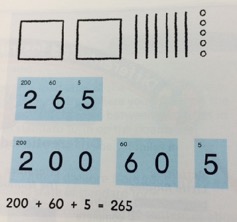
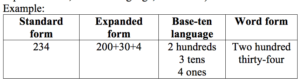
For this reason, we explore many representations of a value. We begin with modeling objects and showing students how they can bundle or put together objects into groups of 10 and place it as 1 in the next greater place value. Then we use these representations to help describe the value in different forms. For example, a value can be written in standard form using digits and placing them in the correct place as in the number 147. Most adults have had experiences writing a number in word form when writing a check. Although many students have never had an opportunity to write a check, and it is uncertain if they ever will, it is still very important that they learn how to write a value in word form because if they know how to write a number they can read a number using proper place value language. Yet, the idea of expanded form or base-ten language are very foreign to many of us. So, why are our students learning this and why is it important?
1. Expanded form- is a way to write numbers by adding the value of its digits. Example: 900 + 50 + 4 = 954.
When looking at a value like 1,954 children often have difficulty understanding place value and the value of each digit. Many children when asked describe each digit as a value of ones. When looking at the example above a child may say that the digit 9 has a value of 9 rather than having a value of 900. When students expand each digit showing its value they gain a deeper understanding of the digit’s worth depending on its place within the number.
2. Base ten language- is a way to use three digits of a three-digit number represent amounts of hundreds, tens, and ones; e.g., 706 equals 7 hundreds, 0 tens, and 6 ones.
The use of base ten language helps students to understand that a digit in a place value represents a grouping rather than just the value of the digit.
Investigating a value in so many ways sets the stage for better addition and subtraction strategies later in the year as well as multiplication and division strategies in third grade.
Check out this Learnzillion video to learn more about different forms of a number.