Compare two decimals to hundredths by reasoning about their size. Recognize that comparisons are valid only when the two decimals refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual model.
[divider] [/divider]Students are able to…
- Compare decimals that are tenths with tenths and hundredths using a strategy that makes sense (base-ten blocks, grids, number lines or fraction numbers) and explain their reasoning using models, pictures, numbers and words.
- Compare decimals that are tenths with hundredths using a strategy that makes sense (base-ten blocks, grids, number lines or fraction numbers) and explain their reasoning using models, pictures, numbers and words.
[divider] [/divider]Students are able to…because teachers…
- Provide opportunities for students to compare tenths written as fractions with: tenths written as decimals, hundredths written as fractions, and hundredths written as decimals to understand that there are different ways to write the same value.
- Provide opportunities for students to use manipulatives, grid paper, number lines, and fractional representations to model and compare tenths and hundredths.
- Connect activities to include numerical representations.
- Ask students to justify their answers.
[divider] [/divider]Questions to ask students:
- How does place value play a role in comparing decimals?
- Sample answer that indicates understanding: The location or place of the digit helps determine it’s value. You have to use place value to correctly compare two decimal amounts.
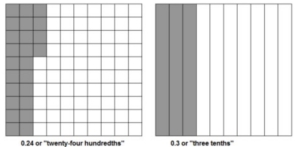
- How can you use a model to compare 0.24 and 0.3?
- Sample answer that indicates understanding: 0.24 < 0.3. 0.3 covers more space in the model. Also, using place value… I can use the tenths place to compare – 3 tenths are greater than 2 tenths.
- How does 0.3 (three tenths) compare to 0.30 (thirty hundredths)? Explain your reasoning.
- Sample answer that indicates understanding: The student correctly answers they are equal and explains or proves their thinking with models or words (ex. Both numbers have a 3 in the tenths place, and draws a model showing 3 tenths covers the same amount as 30 hundredths.)
- Sample answer that indicates an incomplete understanding or a misconception: 30 is greater, because it has 30 and the other decimal has 3.
- How does 5.64 (five and sixty-four hundredths) compare to 5.46 (five and forty-sixth hundredths)? Explain your reasoning.
- Sample answer that indicates understanding: The first place we can use to compare the digits is the tenths place. There are 6 tenths in 5.64 and 4 tenths in 5.46. So 5.64 is greater than > 5.46.
- How can you represent 0.5 and 0.2 on a number line? Use <, =, > to compare the two decimals.
[divider] [/divider]FSA Notes
Cognitive Complexity Level: 2: Basic Application of Skills & Concepts
Achievement Level Descriptors:
2 – compares two decimals with the same number of places (tenths or hundredths) using visual models; recognizes that the decimals must refer to the same whole
3 – compares two decimals to the hundredths (using <, >, and =) by reasoning about their size and justifies using models
4 – determines a decimal that is between two given decimals
5 – [intentionally left blank]
Assessment Limits:
Decimals may reference the same whole entity.
Decimals are limited to tenths and hundredths.
Decimals may be greater than 1.
Items may not require a comparison of visual models in isolation.
[divider] [/divider]Additional Resources:
Additional in depth content knowledge
Video: Compare decimals visually
Compare two decimals to the hundredths place using fraction models
[divider] [/divider]Sample Formative Assessment Tasks:
Resources/Tasks to Help Your Child at Home:
Using a deck of cards, play decimal war. Have your child create a two-digit decimal (to the hundredths place) and you create a two-digit decimal (to the hundredths place). Compare the two decimals, whomever has the greatest decimal wins the round. Prove the comparison with a number line, area model or place value. (Example: Compare using place value: “I have 0.26 and you have 0.62. You have the greatest decimal because I have a 2 in the tenths place and you have a 6 in the tenths place.”) Then record the comparisons using the symbols <, > or =. After 10 rounds, switch to go greater than a whole (using three digits: the ones, tenths and hundredths place).
Khan Academy: Comparing Decimals Visually https://goo.gl/JnmmA6