Why teach math vocabulary?
The Standards for Mathematics emphasize that mathematically proficient students communicate precisely to others; however, the language of mathematics can often be confusing. Lack of knowledge of math vocabulary can hinder achievement.
What makes math vocabulary different from other subjects?
Math vocabulary is unique in that the purpose is to communicate mathematical ideas, so it is necessary to first understand the mathematical idea the language describes. With the new understanding of the mathematical idea comes a need for the mathematical language to precisely communicate those new ideas.
When should you teach math vocabulary?
Introduce the vocabulary only after you have identified the vocabulary to be taught, developed your own understanding of the related math ideas, and then purposefully planned for how to connect the meaning to learning experiences.
While pre-teaching vocabulary may be appropriate for other subjects, since mathematical vocabulary represents a mathematical concept, it does not make sense to teach the word before students understand the concept. Rather, vocabulary words should be introduced to students through active engagement with the math.
Only after students have developed a conceptual understanding and expressed that understanding in their own words should the teacher help students connect the formal vocabulary with their current understanding. Introducing the vocabulary during the lesson connects it to the meaningful math they are doing at the time. It supports the math and allows them to be more precise in their justifications and explanations.
What are some strategies for teaching math vocabulary?
1. Concept Attainment/Concept Card– Having students develop their own definitions helps them focus on key characteristics of concepts, thus building conceptual understanding.
Step 1: Teacher presents students with several examples and non-examples. The teacher may choose to tell students the name of the concept, or may wait to give the formal names to the concepts until after the class has developed a final definition.
Step 2: Students consider first set of examples and non-examples and develop a rough draft of a definition. Initial definition is recorded where class can see it, and everyone has the opportunity to revise it.
Step 3: Additional pairs of examples and non-examples are presented, and with each pair, students revise their definition. Teacher uses questioning and strategically selects and orders the examples and non-examples to facilitate the refinement of the definition.
Step 4: Students create additional examples and non-examples to add to the concept card.
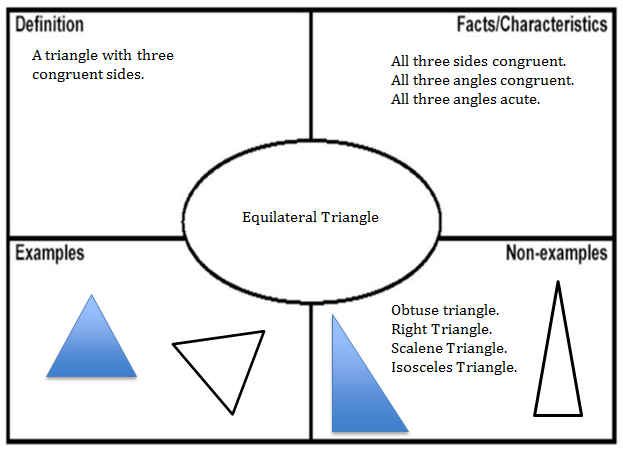
2. Frayer Models- Students identify examples and non-examples of a concept and differentiate between defining and non-defining attributes/characteristics. In an alternate version, they are developing a definition, identifying examples and non-examples, and providing an illustration or characteristics.

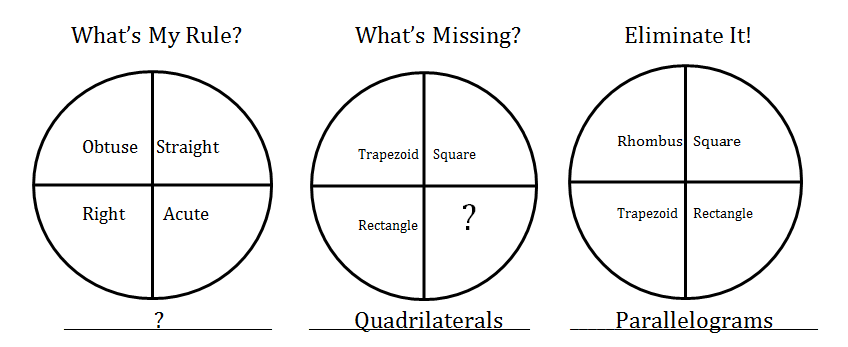
3. Concept Circle/What’s my rule?/Eliminate it! – Students describe the common attributes or name the relationship that exists between the circle in an attempt to label the circle. Students can also be given the label of the circle and asked to provide an additional example. Or, students can be given the label and the circle can include a non-example which students are asked to identify.
4. Discussion (Think-Pair-Share, Turn and Talk, Revoicing)- Keeping in mind the goal of precise communication, it is important that all students engage in using the new language. Using cooperative structures increase participation in the discussion and promote accountability.
5. Journaling- Writing about mathematics not only provides students with another opportunity to understand math language, but it also gives teachers the opportunity to assess student understanding of the terms they use.
6. Interactive Math Word Wall– Word walls encourage discussion and facilitate connections between the vocabulary and the mathematical ideas they represent. Here are some math word wall activities to incorporate into your daily routine:
• Pictionary – Students draw a representation of one of the words for the others to guess.
• Fly Swatter – Give the definition of a word, ask who sees the word, and give that student a fly swatter to swat the word
• I AM/Vocabulary Riddles – Students take turns saying, “I AM……” then fill in the blank using the definition for one of the words. (Ex. “I AM the answer in multiplication.”) The person who identifies the correct word is the next one to take a turn.
For more information on use of the graphic organizers, visit http://oame.on.ca/main/files/thinklit/FrayerModel.pdf