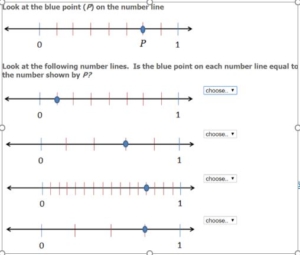
Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size
a. Understand two fractions as equivalent (equal) if they are the same size, or the same point on a number line.
[divider] [/divider]
Students are able to…
- Use visual representations including rectangular and circular area models, fraction bars, and the number line to find various (equivalent fractions) that name the same quantity or point.
- Recognize patterns and make generalization that the same fraction can be named in different ways. On a number line, they would be located at the same point on the number line; in an area model they would represent the same portion of the whole.
- Understand that for fractions to be equivalent, the wholes must be the same.
Students are able to…because teachers:
- Provide a variety of activities with visual models, including area models, fraction strips, and the number line, to give students experience developing conceptual understanding that
- Many fractions can describe the same quantity or point on a number line
- Fractions that represent the same amount are called equivalent fractions.
- Use purposeful questions to help students recognize patterns in equivalent fractions.
- What do you notice about the numerators in equivalent fractions?
- What do you notice about the denominators in equivalent fractions?
- What patterns do you see in the numerators and denominators in two equivalent fractions?
- Present students with problem solving situations that give students the opportunity to realize that fractions are equivalent only when referring to the same whole.
[divider] [/divider]
Questions to ask students:
- Present students with two visual models of one-fourth with different size wholes (see model below). Have students explain whether or not the wholes are equivalent.

- Ask students what it means for two fractions to be equivalent.Sample answer that indicates understanding: Even though both models represent one-fourth, they are not equivalent, because the wholes are not the same size.
- Sample answer that indicates an incomplete understanding or a misconception: They are equivalent, because they both have one-fourth shaded in.
- Sample answer that indicates understanding: The fractions are the same part of the same size whole. On a number line, they would be at the same point, and on an area model they would be the same portion of the whole.
[divider] [/divider]
Achievement Level Descriptors:
Level 2: Identifies equivalent fractions given models;compare two fractions with the same denominator, using visual fraction models, and records results using symbols
Level 3: Generates equivalent fractions; explains why the fractions are equivalent;recognizes and expresses fractions that are equivalent to whole numbers and vice versa; compares two fractions that have the same numerator or same denominator using symbols and justifies the conclusions
Level 4: Generates a fraction that falls between two given fractions with the same numerator or denominator
Level 5: [Intentionally left blank]
[divider] [/divider]
Additional Resources:
-Additional in depth content knowledge:
http://katm.org/flipbooks/3%20FlipBook%20Final%20CCSS%202014.pdf#page=55
-Blog Post: Proving Equivalent Fractions with Models
Proving Equivalent Fractions with Models
-Video: Identify Equivalent Fractions Using Fraction Models https://learnzillion.com/lesson_plans/5164-identify-equivalent-fractions-using-fraction-models
-Identify Equivalent Fractions Using a Number Line https://learnzillion.com/lesson_plans/8141-identify-equivalent-fractions-using-a-number-line
Sample Formative Assessment Task: