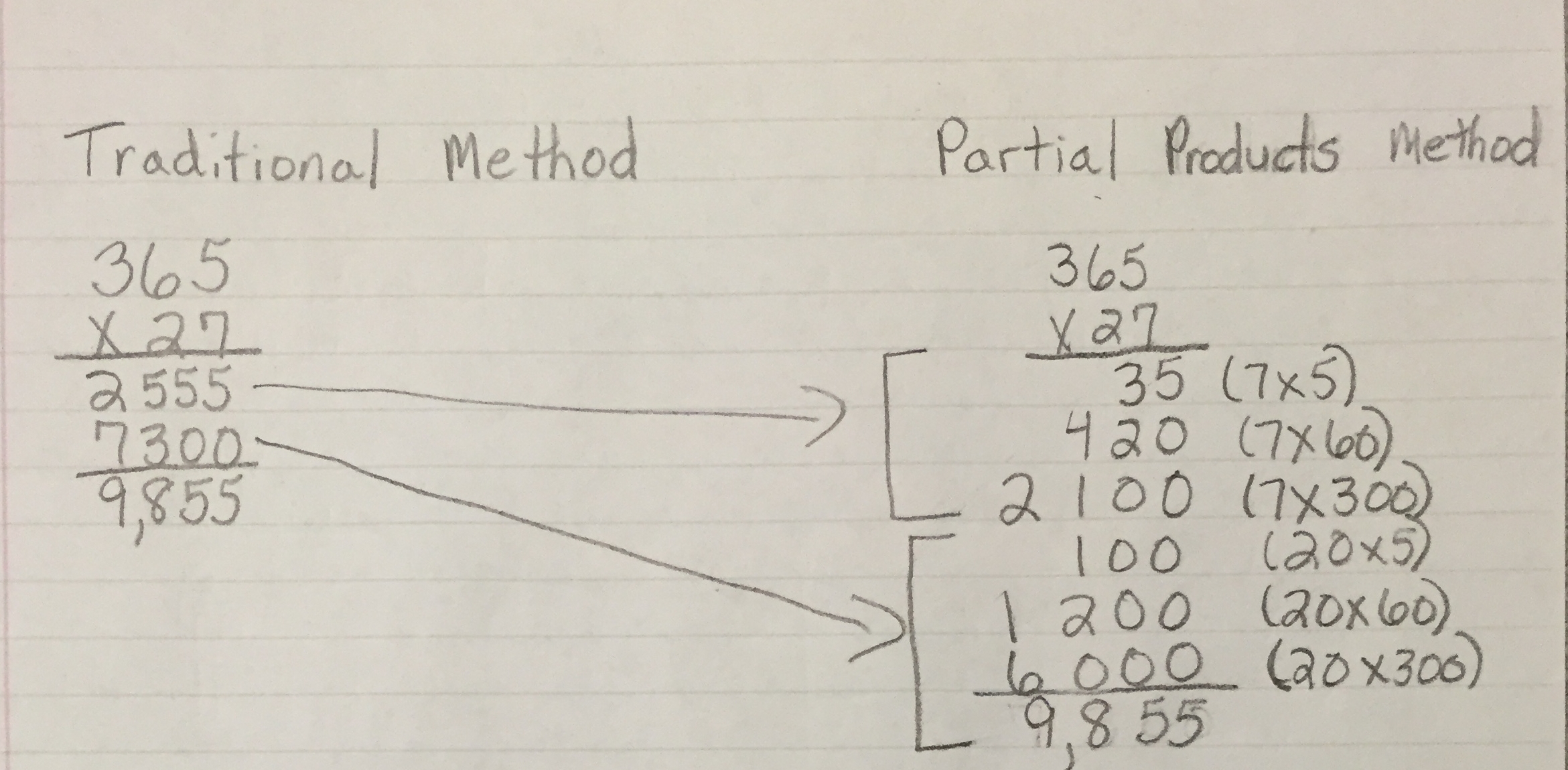
It’s important in grade 5 for students to have a solid understanding of multi-digit multiplication. One way to do that is to make connections between methods. Take for example, the traditional method and the partial products method. Let’s learn a little about each method.
The partial products method consists of all the individual products produced by the multiplication being recorded on separate lines then added. The partial products method can be useful and help students better understand the traditional method which is probably how most of us learned how to multiply.
The traditional method is a version of the partial products method. In the traditional method, some of the partial products are added mentally before the sum is written down. In some instances, the traditional method is more efficient than the partial products method (because it requires less writing). But this method is not as easy to understand step by step and it may be more susceptible to error (because steps are combined and done mentally).
So you’re probably wondering how do I connect these two methods for children?
One way is to use the distributive or break apart strategy. The distributive property helps children understand the relationship between the traditional method and the partial products method. Take our example, 365 x 27, fifth graders should readily think that it could be computed by (365 x 20) + (365 x 7) or in the example 356 x 9 they think (300 x 9) + (50 x 9) + (6 x 9).
Here are some guiding questions to your support your child’s thinking:
Where do you see the partial products recorded in the traditional method?
Why do I add the partial products?
How could you solve 49 x 58 using both methods?