In 3rd grade students are expected to, “Understand a fraction as the quantity formed by 1 part when a whole is partitioned into equal parts.” The best way for students to develop this understanding is by putting fractions into real world context and create area models.
The Top 5 Things Students in 3rd Grade need to understand about modeling fractions with an area model are:
1. Students need to understand when it comes to modeling fractions with an area model, that the parts need to be equal or cover the same amount of space.
For example: A common misconception is shown below. Students need to understand that this is not demonstrating fourths because they are not equal parts.
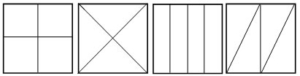
2. Understand that the parts of the whole can be equal without having the same shapes within the whole. A great way to explore this is give students square post-it notes and have them find all the fourths they possibly can. From there – they can prove they are equal by cutting the parts up and comparing the size of the pieces.
The below shapes are common ways that students break squares into fourths because they are the same area and the same shape.
We want students to understand that the below shape is also cut into fourths because they cover the same amount of space or are the same area.
3. Name the equal parts found in the whole as halves, thirds, fourths, sixths and eighths. This occurred in 2nd grade using the language of fractions without using numbers to represent. You want to encourage students to identify shapes broken into each fractional amount.
The below shape is cut into sixths because there are six equal pieces that make up the whole.
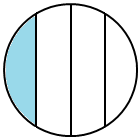
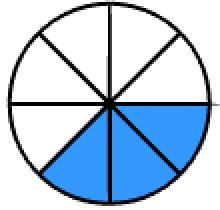
4. The numerator represents the number of pieces being discussed or focused on and the denominator represents the amount of total equal pieces in the whole. At this time students need to be able to represent it in fraction language and numerically as a fraction.
The picture below models 3/8 of the whole as shaded. The numerator 3 represents the number of equal pieces shaded. The denominator 8 represents the total number of equal pieces that make up the whole.
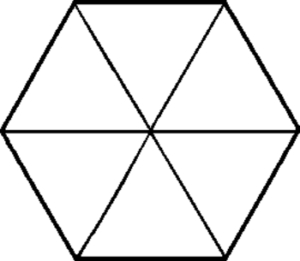
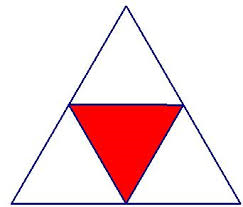
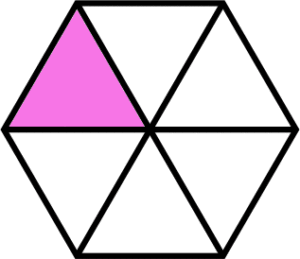
5. Fractions can be found in more shapes than just squares or circles. Students need experiences with determining, creating and identifying fractions in various shapes to know that fractions can be found anywhere in the real world.
Triangle Example:
Hexagon example:
Rectangle example with fraction tiles:
We also want to eventually move students to drawing models of fractions. At this time, you want to encourage discussions about which wholes encourage more precise drawings for modeling specific denominators.
For example: Students are not as precise at drawing thirds in a circle as they are in a square.
For more information on representing fractions with an area model to encourage understanding of fractions, visit https://learnzillion.com/lesson_plans/4930-represent-fractions-in-different-ways or read the article http://lesage.blogs.uoit.ca/wp-uploads/2011/09/Representing-Fractions-NCTM-April-2002.pdf.