Once upon a time long long ago… Just Kidding. A long time ago (like yesterday or the day before) a post came out about base ten and place value. If you didn’t get a chance to check it out just click on this link… http://ow.ly/BYwg3041trZ Its ok, I’ll wait.
Understanding this relationship between place value and multiplication and division we can solve problems more efficiently. Not only that, we will understand what is happening when we are solving these problems.
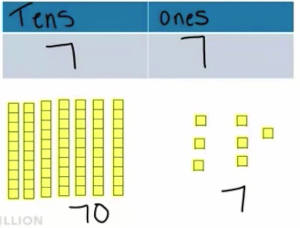
Lets take the number 77. The 7 in the tens represents 7 tens and the 7 in the ones represents 7 ones.
In this model you can see that there are 7 groups of 1 and 7 groups of 10. This is going to help when we are applying multiplication and division because both represent groups. Examples below.
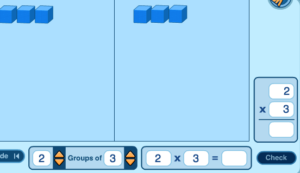
Lets take 2 x 3 or 2 groups of 3 as shown below.
So 2 groups of 3 or 2 x 3 gives us a product of 6. But if you look closely those each block actually represents 1,000.
So what would 2 groups of 3,00 equal? Well of course it equals 6,000. Using what we know about place value can help us not only multiply but also divide.
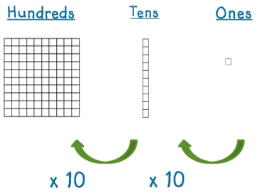
700 divided by 70. I know that there is a 7 in the hundreds place in the number 700 and a 7 in the tens place in the number 70. If I know that each place value to the left is ten time greater than the place value to the right, as shown below.
That mean that 700 is ten times greater than 70 or it would take 10 groups of 70 to equal 700. This could be written as 700 divided by 70 equals 10.
This structure of ten times greater when you move up each place value and ten times less when you move down each place value can really help when multiplying and dividing larger numbers.
For more information on Understanding place value: multiply by a power of 10 check out Learnzillion.com https://learnzillion.com/lesson_plans/6646
For more information on understanding relationships between digits and their place value check out Learnzillion.com https://learnzillion.com/lesson_plans/7426