What is division?
Division is when you know the total amount, and either the number of groups or the size of the equal groups are unknown. Students are expected to understand this process looking at the actions in a story problem and direct modeling what happens to find the quotient. This is presented in various ways to ensure students understand what division is and how it’s related to multiplication.
How should division be introduced?
• Direct modeling with manipulatives – We want students to understand division, so it’s important to have them directly model the actions in a problem using first concrete manipulatives such as counters and then move to drawing quick pictures to directly model the actions in a problem. As students are directly modeling, we want to pose questions to get them to think deeper about what’s happening and how they got their answer. Questions to ask include:
o What do your groups represent?
o What does the dots/cubes in each group represent?
o How does your model relate to the story problem?
Direct Modeling with Counters
Direct Modeling with Base-ten blocks
• In Context – This occurs when you use story problem scenarios that represent division. A story problem could include, “Mark has 24 apples. He gave an equal amount to 3 of his friends. How many apples did each friend receive?”
• Out of Context – This occurs when you present students with an expression to solve, such as 24 ÷3. They can then solve the problem by putting it into context of a story problem to understand the actions.
• Relate to Multiplication – As students are exploring division, they will naturally start seeing similarities to multiplication and division. It’s important to encourage and facilitate these discussions. Some observations may include:
o There are equal groups in multiplication and division
o With division I know the total, with multiplication I don’t
o The model for 24 ÷ 3 looks the same as my model for 3 x 8
How does measurement and partitive division compare?
Measurement and Partitive Division are two types of division that occur based on the type of problem presented. It’s important for children to decontextualize, or break down the problem using the model that directly models the actions in the problem and also represent it with an expression or equation. We want to make sure we expose students to each type of problem, and have them verbalize what they know and what they are trying to find out.
Measurement Division – This type of division occurs when you know the total and how many in each group, but the number of groups is unknown.
Example problem, “Mark has 24 apples. He gave an equal amount to 3 of his friends. How many apples did each friend receive?”
First you would count out 24 “apples” or counters.

Next you would begin separating the “apples” or counters into 3 equal groups.

You would continue to separate the counters into the 3 equal groups until they are either all used or you can no longer create equal groups, then you would have a remainder (which is not addressed in 3rd grade math standards).

Partitive Division – This type of division occurs when you know the total and how many groups, but the number in each group is unknown.
Example problem, “Mark has 24 apples. He gave 3 apples to each of his friends. How many friends received 3 apples?”
First you would count out 24 “apples” or counters.

Next you would begin separating the “apples” or counters into equal groups of 3 apples.

You would continue to separate the counters into equal groups of 3, until they are either all used or you can no longer create equal groups, then you would have a remainder (which is not addressed in 3rd grade math standards).

You want to use the same numbers for partitive and measurement division problems, encouraging students to compare and contrast the two division types. This helps to move students from thinking “I’ll get the same answer anyway,” to “which strategy really directly models the actions in the problem.” This will also help students deepen their understanding of what division is.
What models and strategies can students use to demonstrate an understanding of division?
• Equal groups model with manipulatives – Using Counters or Base ten blocks
I have 24 counters total to separate into equal groups.

I was able to separate the 24 counters into 3 equal groups of 8, so the quotient is 8.

Base ten block models can also be used, which can be a more efficient strategy for modeling division.
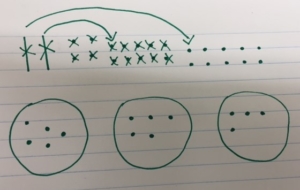
• Equal groups quick picture model – It’s important for students to draw quick pictures, not detailed models
First you begin with create a base ten model of 24, then draw the three groups you will evenly separate the base ten blocks into. You can place one unit into each group.
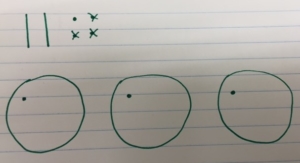
Next you realize you have to break-apart one of the tens into ones to continue to separate the 24 into equal groups.
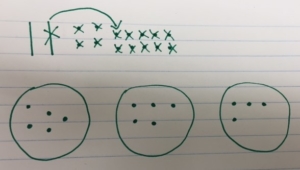
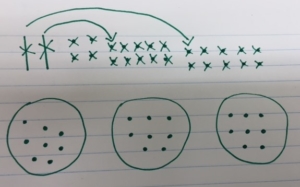
Finally you separate all of the 24 into equal groups. The answer is then 8 which is the quotient, the amount that is in each equal group.
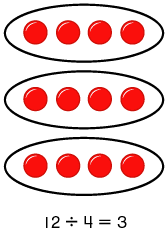
• Number lines – Where you begin with the total, the jumps represent the groups, and the numbers within each jump represent how many in each group.
We began with 24 and then made equal jumps of 3. There were 8 jumps, or equal groups. So 8 is the quotient.
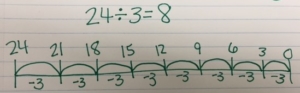
• Arrays – An arrangement of things in rows and columns into a rectangular shape. This can be used with division and multiplication. (There will be another blog that goes into greater detail with this model).
What can I do as the parent to support my child’s understanding of division?
• Encourage use of models. Make sure not to rush your children to solving without models, we want to ensure understanding. With repeated practice and exposure to division, children will naturally become more efficient.
• Ask questions that encourage your child to understand why they created the model they did or helps them think deeper about why they even divided:
o How does your model relate to the problem?
o Equal groups models: What do your groups represent? What do the dots in each group represent?
o Number line model: What does each jump represent? How did you know to begin with the total? What does each number in each jump represent? Why are the numbers decreasing rather than increasing?
o Array models: What does each row/column represent?
For more example division problems visit this website. For more information on understanding division with models visit this website


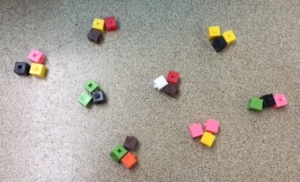
Pingback: Fact Fluency- What is it? | SMathSmarts