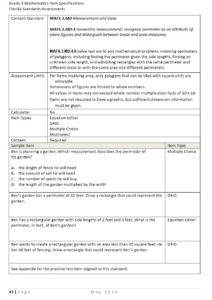
1. What’s included when teaching perimeter in 3rd grade?
• Solving real-world problems involving perimeter of polygons
• Determining when it is necessary to find the perimeter from a given story problem
• Finding the perimeter given the side lengths
• Finding an unknown side length
• Identifying rectangles with the same perimeters
2. Strategies for determining perimeter:
• Counting units
• Use addition/multiplication to determine the perimeter
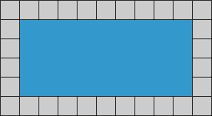
• Measure the perimeter of a polygon using units
• Determining unknown lengths with a given perimeter
• Create a model or picture to determine perimeter of a given polygon
3. Relate Perimeter to the Real World – Put tasks in real world context and make it relevant. Students should learn how perimeter relates to them in their daily life. This will make it more meaningful and accessible for all students.
Example perimeter problem in real-world context: “Students in our class are
having a Thanksgiving feast in the cafeteria. Each long side of the rectangular table we will be using can seat 9 students. Each short side of the rectangular table can seat 3 students. How many students can sit at the table for the Thanksgiving feast?” (Note – to make the task even more relevant actually take students to the cafeteria and problem solve).
4. Hands-on Exploration – Use the concrete-representational-abstract format to help students determine and understand the concept of perimeter.
How do you make it happen? Be careful not to rush students to abstract. You want them to have a solid understanding of what perimeter is through hands-on experiences and exploration. Here is a flow that should be utilized:
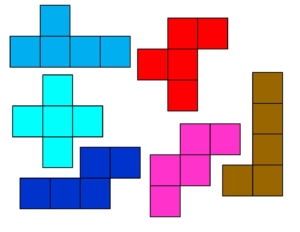
• Concrete – use manipulatives such as square tile and pentominoes to explore counting units around the outside of a figure to determine the perimeter.
• Representational – use graph paper and pictures to explore perimeter on paper.
• Abstract – determine perimeter of a figure by adding or multiplying sides that are of the same length. Encourage students to revisit the attributes of different quadrilaterals to make this happen, specifically rectangles and squares. Example: If one side of a square is 5 centimeters long, I know all sides are 5 centimeters long so I can multiply 4 x 5 to get a perimeter of 20 units.
Fun task to implement – give the students a given perimeter or range of perimeters to look for and have them go around the classroom measuring objects to determine the mystery object(s). Could have them post-it notes or rulers to determine.
Tools to use:
• Square tiles – to represent figures and count to determine perimeter
• Pentominoes – to determine perimeter of irregular figures
• Geoboards – to create or determine perimeter of given polygons
• Graph paper – to represent figures and begin using more efficient strategies for determining the perimeter
• Rulers – to measure the length of figures to determine the perimeter
• Quick pictures – to draw the polygon and determine perimeter from a given problem
5. Precision with units – make sure students are being precise with their measurement units. Have them label the perimeter in units each time they measure. Also have them compare units: “Would a figure with a perimeter of 20 centimeters or 20 meters be larger?”
Consider using the following book title, Racing Around by Stuart Murphy, to explore the concept of perimeter!